QUE ES UN ÁNGULO - MEDICIÓN DE ÁNGULOS - CLASIFICACIÓN DE LOS ÁNGULOS
1. QUÉS ES UN ÁNGULO?
Ángulo es un concepto de la Geometría para referirse al espacio comprendido entre la intersección de dos líneas que parten de un mismo punto o vértice, y que es medido en grados.
La palabra proviene del latín angŭlus, y esta a su vez del griego ἀγκύλος, que significa "encorvado".
En el uso cotidiano, la palabra ángulo también puede utilizarse como sinónimo de rincón (en el sentido de ángulo entrante) como, por ejemplo: “¿En qué ángulo de la sala prefieres poner el sofá?”; de esquina o arista: “Cuidado con los ángulos de la mesa: te puedes golpear”; así como de punto de vista: “¿Ya evaluaste la situación desde todos los ángulos?”
Para la construción de un gran número de ángulos, podemos realizar distintos procedimientos según las herramientas que utilicemos. De esta forma, y según las herramientas que utilicemos, las construcciones serán:
- A. Utilizando el compás.
- B. Utilizando la escuadra y el cartabón.
Para la construción de un gran número de ángulos, podemos realizar distintos procedimientos según las herramientas que utilicemos. De esta forma, y según las herramientas que utilicemos, las construcciones serán:
- A. Utilizando el compás.
- B. Utilizando la escuadra y el cartabón.
2. MEDICIÓN DE ÁNGULOS
A. Utilizando el compás
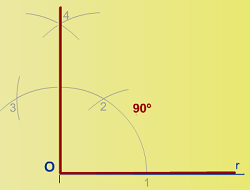
2.2.1. Construcción de un ángulo de 90º.
 OPERACIONES
OPERACIONES
- Desde el punto O de la semirecta Or, utilizando el compás, se traza un arco con un radio cualquiera. El arco corta a la semirecta Or en el punto 1.
- Desde el punto 1, con la misma abertura del compás, se traza un arco, obteniendo el punto 2. De igual manera obtengo el punto 3.
- Utilizando los puntos 2 y 3, realizo otro arco con la misma abertura del compás, obteniendo el punto 4.
- Al unir el punto 4 con el punto O, consigo la recta perpendicular a la semirecta Or en el extremo de la semirecta.
.

OPERACIONES
- Desde el punto O de la semirecta Or, utilizando el compás, se traza un arco con un radio cualquiera. El arco corta a la semirecta Or en el punto 1.
- Desde el punto 1, con la misma abertura del compás, se traza un arco, obteniendo el punto 2. De igual manera obtengo el punto 3.
- Utilizando los puntos 2 y 3, realizo otro arco con la misma abertura del compás, obteniendo el punto 4.
- Al unir el punto 4 con el punto O, consigo la recta perpendicular a la semirecta Or en el extremo de la semirecta.
.
2.2.2. Construcción de un ángulo de 45º.
 Partiendo del ángulo de 90º construido anteriormente, trazamos la bisectriz del ángulo y obtenemos el ángulo de 45º.
.
.
.
.
.
Partiendo del ángulo de 90º construido anteriormente, trazamos la bisectriz del ángulo y obtenemos el ángulo de 45º.
.
.
.
.
.
 Partiendo del ángulo de 90º construido anteriormente, trazamos la bisectriz del ángulo y obtenemos el ángulo de 45º.
Partiendo del ángulo de 90º construido anteriormente, trazamos la bisectriz del ángulo y obtenemos el ángulo de 45º.
.
.
.
.
.
2.2.3. Construcción de un ángulo de 22º 30′.
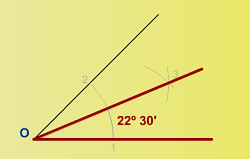 Si nos piden la construcción de un ángulo de 22º 30′, tendremos que fijarnos que esta medida es la mitad del ángulo de 45º. Para construir este ángulo habrá que dividir el ángulo de 45º en dos partes iguales, o lo que es lo mismo, trazar la bisectriz del ángulo de 45º.
.
.
Si nos piden la construcción de un ángulo de 22º 30′, tendremos que fijarnos que esta medida es la mitad del ángulo de 45º. Para construir este ángulo habrá que dividir el ángulo de 45º en dos partes iguales, o lo que es lo mismo, trazar la bisectriz del ángulo de 45º.
.
.
 Si nos piden la construcción de un ángulo de 22º 30′, tendremos que fijarnos que esta medida es la mitad del ángulo de 45º. Para construir este ángulo habrá que dividir el ángulo de 45º en dos partes iguales, o lo que es lo mismo, trazar la bisectriz del ángulo de 45º.
Si nos piden la construcción de un ángulo de 22º 30′, tendremos que fijarnos que esta medida es la mitad del ángulo de 45º. Para construir este ángulo habrá que dividir el ángulo de 45º en dos partes iguales, o lo que es lo mismo, trazar la bisectriz del ángulo de 45º.
.
.
2.2.4. Construcción de un ángulo de 60º.
 Partimos del ángulo de 90º.
OPERACIONES:
Partimos del ángulo de 90º.
OPERACIONES:
- Con una abertura cualquiera del compás y pinchando en el vértice del ángulo de 90º (vértice O), trazamos un arco que corta a la recta r en el punto 1.
- Pinchando con el compás en 1, trazamos un arco CON LA MISMA abertura que habíamos utilizado en el arco anterior. Corta al arco anterior en 2.
- Unimos 2 con el vértice del ángulo (O) y obtenemos el ángulo de 60º.
.
 Partimos del ángulo de 90º.
Partimos del ángulo de 90º.
OPERACIONES:
- Con una abertura cualquiera del compás y pinchando en el vértice del ángulo de 90º (vértice O), trazamos un arco que corta a la recta r en el punto 1.
- Pinchando con el compás en 1, trazamos un arco CON LA MISMA abertura que habíamos utilizado en el arco anterior. Corta al arco anterior en 2.
- Unimos 2 con el vértice del ángulo (O) y obtenemos el ángulo de 60º.
.
2.2.5. Construcción de un ángulo de 30º.
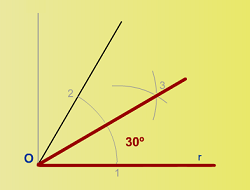 En este caso partimos del ángulo de 60º. Trazamos la bisectriz del ángulo de 60º y obtenemos el ángulo de 30º.
.
.
.
.
.
En este caso partimos del ángulo de 60º. Trazamos la bisectriz del ángulo de 60º y obtenemos el ángulo de 30º.
.
.
.
.
.
 En este caso partimos del ángulo de 60º. Trazamos la bisectriz del ángulo de 60º y obtenemos el ángulo de 30º.
En este caso partimos del ángulo de 60º. Trazamos la bisectriz del ángulo de 60º y obtenemos el ángulo de 30º.
.
.
.
.
.
2.2.6. Construcción de un ángulo de 15º.
 De la misma forma que en el caso anterior, en este caso partimos del ángulo de 30º. Trazamos la bisectriz del ángulo de 30º y obtenemos el ángulo de 15º.
.
.
.
.
De la misma forma que en el caso anterior, en este caso partimos del ángulo de 30º. Trazamos la bisectriz del ángulo de 30º y obtenemos el ángulo de 15º.
.
.
.
.
 De la misma forma que en el caso anterior, en este caso partimos del ángulo de 30º. Trazamos la bisectriz del ángulo de 30º y obtenemos el ángulo de 15º.
De la misma forma que en el caso anterior, en este caso partimos del ángulo de 30º. Trazamos la bisectriz del ángulo de 30º y obtenemos el ángulo de 15º.
.
.
.
.
B. Utilizando la escuadra y el cartabón
También podemos construir un gran número de ángulos utilizado los ángulos proporcionados por la escuadra y cartabón. Sabiendo que la escuadra tiene un ángulo de 90º y dos de 45º y el cartabón tiene ángulos de 30º, 60º y 90º, algunas de las construcciones que se pueden hacer son:
También podemos construir un gran número de ángulos utilizado los ángulos proporcionados por la escuadra y cartabón. Sabiendo que la escuadra tiene un ángulo de 90º y dos de 45º y el cartabón tiene ángulos de 30º, 60º y 90º, algunas de las construcciones que se pueden hacer son:
2.2.7. Construir un ángulo de 22º 30′.
 Partiendo del ángulo de 45 que tiene una escuadra, podemos utilizar este ángulo para, por medio de la bisectriz, conseguir el ángulo de 22º 30′ .
.
.
.
.
Partiendo del ángulo de 45 que tiene una escuadra, podemos utilizar este ángulo para, por medio de la bisectriz, conseguir el ángulo de 22º 30′ .
.
.
.
.
 Partiendo del ángulo de 45 que tiene una escuadra, podemos utilizar este ángulo para, por medio de la bisectriz, conseguir el ángulo de 22º 30′ .
Partiendo del ángulo de 45 que tiene una escuadra, podemos utilizar este ángulo para, por medio de la bisectriz, conseguir el ángulo de 22º 30′ .
.
.
.
.
2.2.8. Construir un ángulo de 75º.
 Podríamos llegar a este ángulo sabiendo que uno de los ángulos de la escuadra es 45º y uno de los ángulos del cartabón es 30º. Sumando ambos, obtenemos el ángulo de 75º.
.
.
.
.
Podríamos llegar a este ángulo sabiendo que uno de los ángulos de la escuadra es 45º y uno de los ángulos del cartabón es 30º. Sumando ambos, obtenemos el ángulo de 75º.
.
.
.
.
 Podríamos llegar a este ángulo sabiendo que uno de los ángulos de la escuadra es 45º y uno de los ángulos del cartabón es 30º. Sumando ambos, obtenemos el ángulo de 75º.
Podríamos llegar a este ángulo sabiendo que uno de los ángulos de la escuadra es 45º y uno de los ángulos del cartabón es 30º. Sumando ambos, obtenemos el ángulo de 75º.
.
.
.
.
 2.2.9. Construir un ángulo de 67º 30′.
2.2.9. Construir un ángulo de 67º 30′.
Si sumamos el ángulo de 90 º del cartabón con los 45º de la escuadra tendremos un ángulo de 135º. Al trazar la bisectriz de este ángulo, obtenemos el ángulo de 67º 30′.
.
.
.
.
.
.
.
.
Si sumamos el ángulo de 90 º del cartabón con los 45º de la escuadra tendremos un ángulo de 135º. Al trazar la bisectriz de este ángulo, obtenemos el ángulo de 67º 30′.
.
.
.
.
.
.
.
.
2.2.10. Construir un ángulo de 7º 30′.
 Al coger el ángulo de 60º del cartabón y quitarle los 45º de la escuadra obtenemos un ángulo de 15º. Al trazar la bisectriz de este ángulo, obtenemos el ángulo que nos piden (7º 30′).
Al coger el ángulo de 60º del cartabón y quitarle los 45º de la escuadra obtenemos un ángulo de 15º. Al trazar la bisectriz de este ángulo, obtenemos el ángulo que nos piden (7º 30′).
VÍDEO CONSTRUCCIÓN DE ÁNGULOS CON AYUDA DEL TRANSPORTADOR
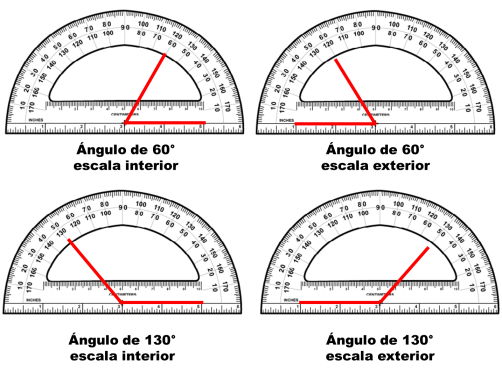
Trazo de ángulos con instrumentos geométricos
Utiliza regla y transportador
Identifica el centro del transportador, el cero de la escala y el origen de la semirrecta que es el lado inicial del ángulo.

Coloca el transportador sobre la línea, haciendo que coincida el inicio de la semirrecta con el centro del transportador y el otro extremo, con el cero de la escala.
 Con ayuda de una regla y partiendo del origen de la semirrecta original del ángulo y del centro del transportador, ubica los grados que va a medir el ángulo en la escala interior del transportador y marca un punto al margen del transportador. Ejemplo 60 °
Con ayuda de una regla y partiendo del origen de la semirrecta original del ángulo y del centro del transportador, ubica los grados que va a medir el ángulo en la escala interior del transportador y marca un punto al margen del transportador. Ejemplo 60 °
 Retira el transportador y con ayuda de la regla, traza la semirrecta final del ángulo haciendo que coincida el origen de la semirrecta inicial del ángulo con el punto que trazaste con tu lápiz. Dale la medida necesaria, el punto sólo es la referencia.
Retira el transportador y con ayuda de la regla, traza la semirrecta final del ángulo haciendo que coincida el origen de la semirrecta inicial del ángulo con el punto que trazaste con tu lápiz. Dale la medida necesaria, el punto sólo es la referencia.

 Al coger el ángulo de 60º del cartabón y quitarle los 45º de la escuadra obtenemos un ángulo de 15º. Al trazar la bisectriz de este ángulo, obtenemos el ángulo que nos piden (7º 30′).
Al coger el ángulo de 60º del cartabón y quitarle los 45º de la escuadra obtenemos un ángulo de 15º. Al trazar la bisectriz de este ángulo, obtenemos el ángulo que nos piden (7º 30′).VÍDEO CONSTRUCCIÓN DE ÁNGULOS CON AYUDA DEL TRANSPORTADOR
Trazo de ángulos con instrumentos geométricos
Utiliza regla y transportador
Identifica el centro del transportador, el cero de la escala y el origen de la semirrecta que es el lado inicial del ángulo.

Coloca el transportador sobre la línea, haciendo que coincida el inicio de la semirrecta con el centro del transportador y el otro extremo, con el cero de la escala.

Con ayuda de una regla y partiendo del origen de la semirrecta original del ángulo y del centro del transportador, ubica los grados que va a medir el ángulo en la escala interior del transportador y marca un punto al margen del transportador. Ejemplo 60 °


Retira el transportador y con ayuda de la regla, traza la semirrecta final del ángulo haciendo que coincida el origen de la semirrecta inicial del ángulo con el punto que trazaste con tu lápiz. Dale la medida necesaria, el punto sólo es la referencia.


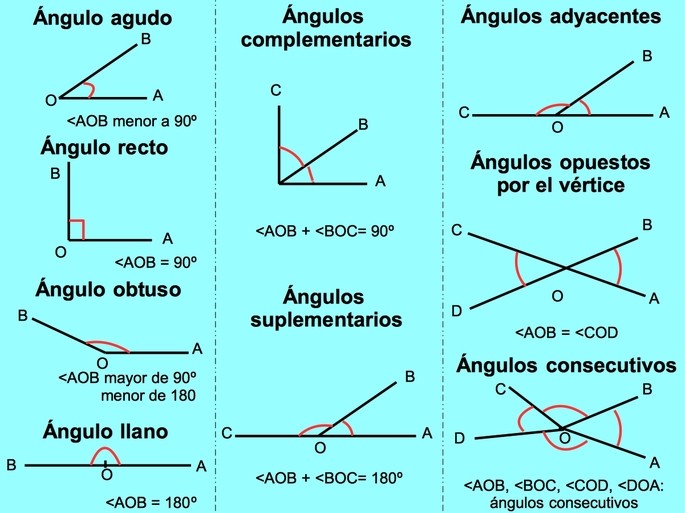
3. CLASIFICACIÓN DE LOS ÁNGULOS
EJEMPLOS DE ÁNGULOS
¡ AHORA! PRACTICA LO APRENDIDO Y RESUELVE:
Realiza los anteriores ejercicios en ´tu cuaderno de actividades de matemáticas:

ACTIVIDAD EN CASA: Crea ángulos:
AGUDOS, OBTUSOS, RECTO, OBTUSO, LLANO, SUPLEMENTARIO y CONSECUTIVOS



Comentarios
Publicar un comentario